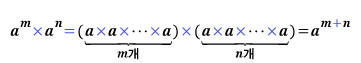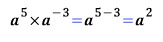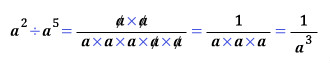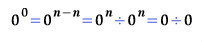라그랑지 포인트 L2

http://commons.wikimedia.org/w/thumb.php?f=Lagrange%20points2.svg&width=2000px


L2위치는 고등학교 물리로 간단히 계산할 수 있단다. 근데 왜 난 간단히 계산이 안될까? 고등학교를 제대로 안나온건 아닌데...

아래 그림을 보고 간단히(?) 계산해보자!!!!

그림에서 x가 L2 위치이고 다음 2가지 조건을 고려하면 된단다.

1) x가 받는 총중력(구심력)은 뛰쳐나가려는 힘(원심력)과 같다.
2) x의 공전주기는 E의 S에 대한 공전주기와 같다.

위의 두식에서 회전각속도   가 같으므로(공전주기 같다는 2번째 조건) 두식은 다음과 같이 변형된다.

문제는 여기까지가 한계라는 것....

댓글들을 참조하여, M은 M끼리 R은 R끼리 정리하면,

식을 간단히 하기 위해

를 이용한다.

여기서 문제는 빼는 항에 t가 분모에도 있다는 것이다.

더하는 항에 t³까지 있고 t<< 1이므로 빼주는 항에 대한 t³까지 근사식을 구한다. 즉, (1+t)^-2의 일차 근사식을 구한다. (테일러 전개 이용)

따라서,

우리가 구하고자 하는 것은 r이므로

물리학의 표준모형

뉴턴이 위대한 과학자로 추앙 받는 이유는 그가 보편적인 중력법칙을 발견했기 때문이다. 그래서 그의 중력법칙에는 만유인력의 법칙(universal law of gravitation)이라는 이름이 붙었다. 질량이 있는 두 물체 사이에는 만유인력이 있는데, 이는 각 질량의 곱에 비례하고 거리의 제곱에 반비례한다는 만유인력의 내용을 다들 한번씩은 들어봤을 것이다. 지금 생각해 보면 뭐가 그리 대단할까 싶기도 하지만 ‘과학’이라는 단어 자체가 없었던 17세기에는 사정이 달랐다. 지구와 태양 사이에 작용하는 것과 똑같은 힘이 지상의 모든 물체에도 작용하며 더 나아가 우주의 삼라만상이 모두 같은 힘의 지배를 받는다니, 보통 사람으로서는 쉽게 생각하기 어렵다.

 

 

 

과학자들은 비교적 단순하다. 자연현상은 복잡해도 그 내면의 근본원리는 그다지 복잡하지 않으리라고 생각한다. 그러자면 두루두루 적용되는 보편성을 추구할 수밖에 없다. 이렇듯 과학자들은 한두 가지의 보편적인 원리로 수많은 자연현상을 설명하는 것을 좋아한다. 어쩌면 그것이 과학을 하는 최고의 보람인지도 모른다. 우리가 관찰하는 모든 현상들마다 제각각 적용되는 작동원리를 과학자들이 보편법칙이라고 내놓는다면 무척 실망스러울 것이다. 보편성을 추구하는 과학자들의 열망은 일종의 본능이다. 아인슈타인 역시 이 본능에 가장 충실했던 사람 중 한 명이었다. 말년의 그는 통합이론(대통일이론)에 관심이 많았다. 당시까지 알려져 있던 중력과 전자기력을 하나의 이론으로 설명하고자 했다. 안타깝게도 아인슈타인의 노력은 실패했지만 보편적 진리를 추구했던 그의 열정과 노력은 후대의 과학자들에게 면면히 이어졌다.     지금까지 인간이 알고 있는 자연계의 힘은 네 가지이다. 중력, 전자기력, 약력, 강력이 그들이다. 현대적인 이론에서는 이 네 가지 힘에는 각각의 힘을 매개하는 입자가 있다고 이해하고 있다. 중력자(중력), 광자(전자기력), W 및 Z(약력), 접착자(강력)가 그들이다. 한편 자연계에는 힘을 매개하는 입자 외에 물질을 구성하는 구성입자들이 있다. 전자나 양성자 등이 이에 속한다. 중력은 질량이 있는 두 물체 사이에 작용하는 힘이다. 즉, 물체가 지구로 떨어지게 만드는 가장 친숙한 힘이다. 뉴턴이 중력을 만유인력의 법칙으로 정식화했고 아인슈타인은 일반상대성이론으로 현대화했다. 전자기력은 전기력과 자기력을 함께 일컫는다. 전자기력은 고대부터 알려져 있었다. 전기력과 자기력이 하나의 힘이라는 사실은 패러데이(Michael Faraday, 1791~1867)가 전자기유도현상을 발견함으로써 확실해졌다. 전자기력은 맥스웰(James Clerk Maxwell, 1831~1879)에 이르러 그의 유명한 방정식으로 총정리 되었다. 약력과 강력은 원자핵을 발견한 뒤 그 성질들을 연구하면서 알게 된 힘이다.

 

 

약력(약한 핵력, 혹은 약한 상호작용)을 발견하게 된 계기는 베타붕괴라 는 현상 덕분이었다. 베타붕괴는 중성자가 전자를 방출하면서 양성자로 바뀌는 현상이다. 이 과정에서 무엇인가 전에는 알지 못하던 힘이 작용하는 것이 아니냐는 생각이 들었다. 이 힘을 연구해보니 이 힘은 중력보다는 강하지만, 전자기력보다는 약했다. 그래서 약력이라고 부르게 되었다. 중성자가 붕괴할 때는 아주 이상한 현상이 생긴다. 원래 중성자가 가졌던 에너지와 베타 붕괴 이후에 전자와 양성자가 가지는 에너지가 서로 다르다. 즉, 가장 기본적인 에너지 보존법칙이 맞지 않는 것처럼 보인 것이다. 이 문제를 해결한 사람은 볼프강 파울리이다. 볼프강 파울리는 질량이 거의 없고 전기적으로 중성인 입자가 이 반응에 참가하여 에너지를 가지고 달아난다면 에너지 보존 문제를 해결할 수 있다고 생각했다. 전기적으로 중성이면서 매우 가벼운 이 입자를 중성미자(neutrino)라고 한다. 중성미자는 약력에만 관여하는 입자이다.

 

 

강 력(강한 핵력, 혹은 강한 상호작용)을 발견하게 된 이유는 간단하다. 수소 이외의 원자핵은 두 개 이상의 양성자로 구성되어 있다. 양성자는 모두 전기적으로 양성이라 양성자가 여럿 모여 있으면 전기적인 반발력이 대단할 것으로 쉽게 예상된다. 따라서 전자기력보다는 훨씬 강한 힘으로 원자핵을 구성하는 양성자와 중성자를 묶어줄 힘이 필요하다. 전자기력은 약력이나 중력 보다 센 힘이니, 전자기력 보다 강한 힘이 필요하다. 그래서 강력이라는 개념이 생겨났다. 일본인 최초로 노벨상을 수상한 유카와 히데키(湯川秀樹, 1907~1981)는 양성자나 중성자들이 중간자(meson)라는 새로운 입자들을 교환하면서 강력을 형성한다고 생각했다. 그의 예언대로 파이온(pion)이라는 중간자가 1947년 발견되었다. 즉, 강력은 새로운 힘이고, 전자기력 보다 강한 힘이며, 중간자가 관여하는 힘이라는 것을 알게 된 것이다.

 

 

중성자와 양성자는 더 이상 쪼갤 수 없다는 의미에서의 기본 소립자는 아니다. 이후 양성자나 중성자가 쿼크(quark)라는 더 작은 입자들로 이루어졌다는 증거들이 발견되었다. 쿼크는 머리 겔만(Murray Gell-Mann)과 츠바이히(George Zweig)가 1963년 독립적으로 제시한 개념이다. 쿼크 셋이 적당히 잘 모이면 양성자나 중성자가 된다. 또한 강력에 관여하는 중간자도 쿼크로 구성되어 있다는 것이 밝혀졌다. 양성자나 중성자, 중간자는 모두 강력과 관계가 있다.   더 연구를 진행해 본 결과 쿼크는 강력을 느끼는 최소 입자 단위이고, 쿼크와 쿼크는 접착자(gluon)라고 불리는 강력의 매개체를 주고받으며 강하게 결합해서 양성자나 중간자를 만든다는 것이 알려졌다. 쿼크는 총 6종이 있다고 밝혀졌다. 6종류의 쿼크는 2가지씩 짝을 이룬다. 그 이름은 업(Up)/다운(Down), 참(Charm)/스트레인지(Strange), 톱(Top)/보텀(Bottom)이다.

 

 

양성자, 중성자가 강력으로 뭉쳐져서 원자핵을 만든다는 것은 앞에서 설명하였다. 그러면 전자들도 뭉쳐질 수 있을까? 강력은 전자기력보다 강하므로 전자들 사이에도 강력이 작용할 수 있다면 전자들도 여러 개 뭉쳐질 수 있을 것이다. 그러나 이런 일은 생기지 않는다. 전자는 강력을 느끼지 못하기 때문이다. 전자와 중성미자는 약력에는 반응을 하는데, 강력은 느끼지 못한다. 이런 입자들을 경입자라 고 한다. 경입자는 강력을 느끼는 쿼크와는 전혀 종류가 다른 입자인 셈이다. 경입자도 총 6종이 발견되었다. 처음에 발견된 중성미자는 약력과 반응할 때 전자와 관련되기 때문에 전자형 중성미자라고 한다. 이와 비슷하게 뮤온(muon)이라는 경입자에는 뮤온형 중성미자가 있고, 타우온(tauon)이라는 경입자에는 타우온형 중성미자라는 것이 있다. 전자와 뮤온 혹은 타우온은 질량만 다를 뿐 그 외 모든 물리적 성질은 똑같다. 말하자면 전자의 형제뻘 되는 입자들이다. 그 각각의 짝을 이루는 중성미자들도 서로 형제뻘이다. 약력은 W, Z로 불리는 입자들이 매개한다는 것이 밝혀졌다. 요약하자면 이렇다. 자연계의 소립자는 크게 힘을 매개하는 입자와 물질을 구성하는 구성입자로 나뉜다. 구성입자는 다시 강력을 느끼는 쿼크와 강력을 느끼지 못하는 경입자로 구분된다.

 

 

자 연에는 왜 네 개나 되는 힘이 존재하는 것일까? 초등학생이 던질 법한 이 질문에 아직 우리는 만족할만한 답이 없다. 아마 이 질문은 21세기에도 과학의 최대 난제 중 하나로 남을 것 같다. 자연의 근본이치를 묻는 사람들이라면 응당 네 개의 힘이 별개로 존재한다기보다 하나의 통합된 힘이 네 개로 갈라졌다는 스토리를 더 좋아할 것이다. 그것은 곧 과학자들의 마음이기도 하다. 통합을 향한 큰 진전이 이뤄진 것은 1960년대였다. 미국의 셸던 글래쇼(Sheldon Glashow)와 파키스탄의 압두스 살람(Abdus Salam), 미국의 스티븐 와인버그(Steven Weinberg)가 그 주역들이었다. 이들의 이름을 딴 GSW 모형은 약한 핵력과 전자기력을 성공적으로 통합했다. 그리고 이와 유사한 이론이 강력을 설명하기 위해 도입되었다. 미국 듀크 대학 교수인 한무영 박사가 지난 2008년 노벨상 수상자인 난부 요이치로와 함께 이 과정에서 크게 기여했다.

 

 

약력과 전자기력, 그리고 강력에 대한 이런 이론들을 한데 모아 사람들은 표준모형이 라고 부르기 시작했다. 표준모형은 강력을 느끼지 못하는 세 쌍의 경입자들과 강력도 함께 느끼는 세 쌍의 쿼크들, 그리고 세 가지 힘을 매개하는 입자들에 관한 이론이다. 지난 40여 년 동안 표준모형은 다양한 실험적 검증을 통해 가장 믿을 만한 이론적 체계로서 아직 그 자리를 지키고 있다. “세상은 무엇으로 만들어졌을까?”라는 인류 태고의 질문에 대한 모범답안이 바로 표준모형이다. 그러나 표준모형에서 가장 중요한 입자가 아직 실험적으로 발견되지 않고 있어 많은 과학자들의 애를 태우고 있다. 그것은 바로 힉스(Higgs) 입자이다. 힉스는 표준모형의 가장 핵심적인 연결고리이기 때문에 힉스가 없으면 표준모형은 한마디로 ‘대략 난감’의 상태에 빠진다. 그 난감한 상황이란 무엇일까? 왜 힉스가 꼭 있어야만 하는 것일까? 거기에는 자연의 뒷면에 감춰진 놀라운 비밀과 경이로운 아름다움이 숨어 있다.

 

 

 

 

  출처: http://navercast.naver.com/science/physics/120

0의 0제곱은?

어떤 수의 0 제곱은 1이라고 배웠다. 그런데, 한편으로 0의 거듭제곱은 언제나 0이라고 한다. 그렇다면 0⁰의 값은 0일까, 아니면 1일까?

 

 

윈도에 내장되어 있는 계산기(공학용 보기를 이용)를 이용해서 0의 0제곱을 계산해 보면 1을 출력한다. 인터넷에서 계산기 찾아서 이용해도 같은 결과가 나온다. 그렇다면 00=1일까?       한편, 업무용 프로그램인 엑셀(Excel)에 0의 0제곱을 입력하면 오류 메시지가 출력된다. 수학용 프로그램으로 유명한 매스매티카(Mathematica)에서도 00을 “Indeterminate(정할 수 없는, 不定)”로 처리한다.     어떤 프로그램에서는 00을 1로 처리하고, 어떤 프로그램에서는 처리할 수 없다고 하니, 심지어 같은 회사가 만든 프로그램에서도!  참으로 이상한 일이 아닐 수 없다. 전혀 궁금하지 않다는 사람들도 많겠지만, 00을 무엇으로 생각해야 할지는 역사적으로 오랫동안 논쟁 및 고민거리의 하나였다.

 

 

“거듭제곱”이란 “거듭하여 자신을 곱한다”는 뜻인데, 세 번 거듭 곱하거나, 스무 번 거듭 곱하는 것은 누구나(?) 무슨 뜻인지 안다. a가 수일 때 a를 n개 곱한 것을 an으로 나타내는데, 지수 n이 자연수일 때는 그 뜻이 분명하다. 따라서 이 표기법에 따르면 지수 n이 자연수인 한 당연히 0n=0 이다. 그렇다면 지수가 0이나 음수인 경우는 어떻게 될까? a를 0개 곱하거나 -3개 곱하거나 할 수는 없으므로 곧이곧대로는 정의할 수 없다. 따라서 ‘음수끼리 곱하면 양수’라는 설명을 했을 때와 마찬가지로, 어떻게 정의하는 것이 합리적인지 생각해 볼 필요가 있다. 그 열쇠를 쥔 것은 m과 n이 자연수일 때 성립하는 다음 등식, 즉 ‘지수 법칙’이다.                                              이 지수법칙이 음의 지수에 대해서도 성립하도록 a-3같은 것을 정의하려면, 다음과 같은 등식이 성립하는 것이 좋을 것이다.     양변을 a5으로 나눠주면, a-3은 a2÷a5 임을 알 수 있다. 이 때 문제가 하나 있는데 양변을 a5으로 나누려면 이 수가 0이 아니어야 한다. 만약 a=0이라면 이런 논법이 통하지 않는다. a가 0이 아닐 때는 다음과 같다.     이렇게 음수와 0에 대해서도 지수를 정의해 주면 (밑이 0일 때는 제외하고) 고맙게도 지수법칙 am×an=am+n이 여전히 성립한다. 예를 들어, a-3×a-4=a-7임을 확인할 수 있다. 거듭제곱과 지수의 관계에 대한 이상의 설명에서 알 수 있듯, 자연수 n에 대하여 0n=0이고, 0이 아닌 수 a에 대하여 a0=1이지만, 밑과 지수가 모두 0인 00에 대해서는 아무런 정보도 주지 않는다. 그렇다면 00은 어떻게 정의하는 것이 합리적일까? 과연 합리적인 정의라는 게 가능하기는 한 걸까?

 

 

특히 다항식과 관련한 경우, 00을 1로 두면 수식이 간단해지는 경우가 많다. 예를 들어 다음과 같은 다항식을 생각해 보자.    여기에서 x3은 3차항, -5x2은 2차항이다. 7x는 1차항인데, 7x1이라 쓰면 차수를 알 수 있게 해 주므로 일관성이 있다. 남아 있는 상수항 2는 0차항으로 생각하는 것이 합리적이므로 2x0이라 쓰는 것이 편리할 것이다. 따라서 차수를 고려해서 다항식을 표현하면, 아래와 같이 쓸 수 있다.     원래 다항식에 x=0을 대입하면 당연히 값이 2인데, 차수를 밝혀준 식에 대입할 경우 00= 1이어야 양변이 일치한다! 따라서 00= 1이라고 보는 것이 합리적이다.

 

 

이처럼 극한 이론이 발전하면서 00=1로 간주하자는 주장이 크게 공감을 얻었다. 물론 모두가 그런 것은 아니어서, 예를 들어 프랑스의 위대한 수학자로 극한 이론을 엄밀하게 정립한 코시(Augustin Cauchy, 1789-1857)는 1821년에 쓴 저서에서 여전히 00은 정의할 수 없는 것으로 분류하였다.

 

 

1830년대에 이탈리아의 수학자 리브리(Gulielmo Libri, 1803-1869)는 00=1을 증명하는 논문을 썼는데 내용이 다소 명확하지 못하여, S라는 서명으로만 알려진 익명의 수학자의 비판을 받았다. 우리에게 “뫼비우스의 띠”로 유명한 독일의 수학자 뫼비우스(F. Möbius, 1790-1868)는 얼마 후 리브리의 주장을 옹호하는 논문을 한 편 발표하였는데, 그의 주장은 다음과 같다.

 

 

가끔 a0=1에 대하여 “거듭제곱은 1에 어떤 수를 곱하는 과정이다. 그런데 지수가 0이면 아무것도 곱하지 않았다는 뜻이므로 그 값은 1이 될 수밖에 없다”는 식으로 설명하는 사람을 볼 수 있다. 이것이 거듭제곱을 이해하는 한 가지 방편일 수는 있겠으나, 엄밀히 말하면 앞뒤가 바뀐 설명이다. 거듭제곱을 이런 식으로 생각하는 것은 “a0=1이므로 an은 (지수 법칙에 따라) 1에 a를 n번 곱하는 것이다”와 같은 말이다. 즉, a0=1을 가정한 상태에서 하는 설명이므로, 이로부터a0=1이 된다고 말하는 셈이다. 따라서 이런 설명을 이용해서 00= 1이라고 주장하는 것은 옳지 않다.

 

 

수식도 많고, 글도 길어져서 필자도 미안하게 생각한다. 읽기 힘든 분을 위하여 마무리를 겸하여 내용을 요약하면 다음과 같다. 1. 00은 정의하지 않는다. (값을 아직도 모른다는 말이 아니다.) 2. 그렇지만 ‘주의하여 사용한다면’ 편의상 00= 1로 정의할 수 있다. 3. 위대한 수학자도 실수할 때가 있다.

 

 

 

관련글 :  -1×-1 = 1인 이유는?

 

출처: http://navercast.naver.com/science/math/226

특수 상대성 이론

갈릴레오 갈릴레이(Galileo Galilei, 1564~1642)는 1632년에 「두 체계에 관한 대화」라는 책을 출판했다. 코페르니쿠스의 태양 중심 천문체계와 프톨레마이오스의 지구 중심 천문체계를 비교한 이 책에서 갈릴레이는 밖을 볼 수 없는 갑판 아래의 방에서는 어떤 실험을 하더라도 배가 움직이고 있는지 서 있는지를 알아낼 수 없다고 설명했다. 그것은 서 있는 상태와 같은 속도로 달리는 상태는 물리적으로 동등하다는 것을 뜻한다. 다시 말해 우주 공간에 나만 남고 모든 것이 사라져 버린다면 내가 서 있는지 달리고 있는지 알 수 있는 방법이 없다는 뜻이다. 서 있다거나 달린다는 것은 상대방과의 거리가 어떻게 변하는지를 나타내는 상대적인 개념일 뿐이기 때문이다.

 

 

물리 법칙은 물리량 사이의 관계를 나타낸다. 따라서 물리 법칙이 있기 위해서는 물리량이 있어야 한다. 물리량은 측정된 양이다. 물리학이 수학과 다른 것은 수학은 정의된 양 사이의 관계를 다루고 물리량은 측정된 양(측정 가능한 양)들 사이의 관계를 다룬다는 것이다. 따라서 어떤 양이 물리량이 되기 위해서는 객관적인 측정 방법이 제시된 양이어야 한다. 두 가지 다른 상태가 물리적으로 동등하다는 것은 두 상태에서 측정한 물리량들 사이의 관계를 나타내는 물리법칙이 같다는 뜻이다. 따라서 물리량들 사이의 관계를 알아보는 어떤 실험을 해도 정지해 있는지 달리고 있는지를 알 수 없다.

 

이런 원리를 우리는 상대성 원리라고 한다. 빠르게 달리고 있는 지구 위에서 우리가 편안하게 살아갈 수 있는 것은 상대성 원리 때문이다. 이러한 상대성 원리를 바탕으로 뉴턴역학의 기본이 되는 갈릴레이 상대론이 성립되었다. 갈릴레이의 상대론에서는 정지해 있으면서 측정한 물리법칙과 달리면서 측정한 물리법칙이 같을 뿐만 아니라 물리량도 같아야 한다고 했다. 갈릴레이 상대론에 의하면 측정하는 사람의 상태에 따라 달라지는 양은 속도뿐이어야 한다. 달리고 있는 자동차에서 측정한 기차의 속도와 서 있는 사람이 측정한 기차의 속도가 다르다는 것은 우리 모두가 경험을 통해 잘 알고 있는 사실이다. 속도가 측정하는 사람의 상태에 따라 달라지는 것은 속도는 상대방과의 거리의 변화를 나타내는 양이기 때문이다. 갈릴레이 상대론은 우리가 일상 경험을 통해 알고 있는 사실을 물리학적으로 표현한 것이라고 할 수 있다.

 

 

독일에서 태어나 독일에서 고등학교를 다니고 있던 아인슈타인(Albert Einstein, 1879~1955)은 고등학교를 중퇴하고 사업을 위해 이탈리아로 이사해 살고 있던 부모님을 찾아갔다. 부모님들은 아인슈타인을 설득해 스위스의 취리히 연방 공과대학에 진학하도록 했다. 아인슈타인은 수학이나 물리학에서 뛰어난 재능을 보이기도 했지만 모범적인 학생은 아니었다. 후에 아인슈타인의 상대성이론을 수학적으로 완성하는 데 중요한 역할을 했던 민코프스키 교수는 그에게 게으른 강아지라는 별명을 붙여 주었다. 교수들에게 인정받지 못했던 아인슈타인은 대학원 진학에 필요한 추천서를 받지 못해 대학원에 진학하지 못하고 베른에 있는 특허 사무소에 취직했다.

 

아인슈타인이 학교를 다니는 동안에 미국의 마이컬슨(Albert Abraham Michelson, 1852~1931)과 몰리(Edward Williams Morley, 1838~1923)는 정밀한 측정을 통해 빛의 속도가 지구의 공전 속도의 영향을 받지 않고 항상 일정한 값을 가진다는 것을 밝혀냈다. 아인슈타인이 특수상대성이론을 완성하기 전에 마이컬슨과 몰리의 실험 결과를 알고 있었는지에 대해서는 확실하지 않다. 아인슈타인이 자신이 이에 대해 조금씩 다른 이야기를 했기 때문이다. 갈릴레이 상대론에 의하면 관측자의 상태에 관계없이 속도를 제외한 모든 물리량은 같은 값으로 측정되어야 하고 이들 사이의 관계를 나타내는 물리법칙도 같아야 한다. 그러나 빛의 속도가 모든 관측자에게 같게 관측된다는 것은 이러한 갈릴레이의 상대론이 옳지 않다는 것을 뜻한다. 그것은 200년 동안 가장 완전한 물리법칙으로 생각해 온 뉴턴역학이 틀렸다는 것을 뜻하는 것이었다.

 

물리학자 들은 이 문제를 해결하기 위해 여러 가지 아이디어를 제안했다. 그러나 어떤 제안도 모든 문제들을 한꺼번에 해결할 수는 없었다. 그들의 제안은 대부분 기존의 물리체계 안에서 문제를 해결하려는 것들이었다. 그러나 특허 사무소에서 물리학계와는 거의 아무런 관계를 갖지 않은 채 생활하고 있던 아인슈타인은 기존의 물리체계에 얽매일 필요가 없었다. 1905년 그는 모든 문제를 해결할 수 있는 획기적인 제안을 했다.

 

 

그는 정지해 있는 상태나 같은 속도로 운동하는 관측자에게 같은 물리법칙이 성립되어야 한다는 상대성 원리를 받아들였다. 그리고는 빛의 속도는 누구에게나 항상 같은 값으로 측정된다는 광속 불변의 원리를 받아들였다. 그리고 이 두 가지가 사실이기 위해서는 서로 다른 관성계에서 측정한 물리량이 달라야 한다고 제안했다. 그리고는 정지한 상태에 있는 관측자가 측정한 물리량을 일정한 속도로 달리고 있는 관측자가 측정한 물리량으로 환산하는 환산식을 제안했다. 이 식이 바로 로렌츠 변환식이다.   아래에 나타낸 로렌츠 변환식은 정지해 있는 관측자가 측정한 물리량을 v의 속도로 x방향으로 달리는 관측자가 측정한 양으로 환산하는 식이다.

 

그러니까 아인슈타인의 특수상대성이론은 한 마디로 말해 모든 관성계에서 같은 물리법칙이 성립하고 빛의 속도가 일정하기 위해서는 서로 다른 운동 상태에 있는 관측자가 측정한 물리량이 달라야 한다는 이론이라고 할 수 있다. 상대성 원리와 빛의 속도를 위해 물리량을 희생시킨 이론인 것이다. 빛의 속도와 물리량 모두를 지킬 수 없다는 것을 알게 되었을 때 아인슈타인은 과감하게 빛의 속도를 선택했던 것이다.

 

 

이렇게 보면 특수상대성이론은 참 간단한 이론 같아 보인다. 하지만 여기에는 우리가 받아들이기 어려운 여러 가지 사실이 포함되어 있다. 두 다른 상태에 있는 관측자에게 같은 물리법칙이 성립하고 빛의 속도가 일정하도록 하기 위해 물리량을 변화시키다 보면 우리가 절대 변하지 않을 것이라고 생각했던 물리량도 변해야 한다. 관측자의 상태에 따라 길이가 다르게 측정된다는 것은 그래도 쉽게 받아들일 수 있다. 그러나 시간과 질량마저 다른 값으로 측정되어야 한다는 데 이르면 깜짝 놀라지 않을 수 없다. 그것은 우리가 가지고 있는 시간과 공간에 대한 기본적인 생각마저 바꾸지 않으면 상대성이론을 받아들일 수가 없다는 것을 뜻한다. 오랫동안 과학자들은 시간은 우주에서 일어나는 사건들과는 관계없이 일정하게 흐르는 것이라고 생각했다. 다시 말해 시간의 흐름 속에서 우주가 생겨나고 진화하고, 생명체가 나타나는 사건들이 일어난다고 생각한 것이다. 그러나 이제 시간마저도 관측자의 상태에 따라 달라지는 상대적인 양이 되어 버린 것이다.

 

 

다른 상태에 있는 두 관측자에게 똑같이 운동량 보존 법칙이 성립하려면 질량도 관측자의 속도에 따라 달라지는 양이어야 한다. 속도가 빨라져서 빛의 속도에 다가가면 질량은 엄청나게 커진다. 정지해 있는 물체에 에너지를 가해 속도를 높이면 물체의 운동에너지가 증가한다. 뉴턴역학에서는 질량은 일정한 채 속도가 증가하여 운동에너지가 증가한다고 설명했다.   그러나 특수상대성이론에 의하면 속도가 빨라지면 질량이 증가해야 한다. 따라서 물체에 가해준 에너지의 일부는 속도를 빠르게 하는데 사용되지만 일부는 질량을 증가시키는데 사용된다. 다시 말해 에너지가 질량으로 변환될 수 있다는 것이다. 질량과 에너지 사이의 이런 관계를 나타내는 것이 우리가 잘 알고 있는 E=mc2이라는 식이다.

 

 

상식으로 받아들이기 어려운 이런 내용 때문에 상대성 이론은 오랫동안 많은 사람들의 논쟁의 대상이 되었다. 그러나 현재 특수상대성이론은 여러 가지 장치를 설계하거나 실험을 할 때 없어서는 안 되는 중요한 이론이 되었다. 특히 빛의 속도와 비교할 수 있을 정도로 빠른 속도로 운동하는 입자들을 다루는 입자 가속기의 설계와 제작에는 특수상대성이론을 적용하지 않으면 안 된다. 1905년에 발표된 특수상대성이론은 기존의 역학 체계를 뒤흔드는 혁명적인 이론이었다. 그것은 시간과 공간에 대한 우리의 이해를 새롭게 한 사건이었다. 그러나 아인슈타인은 여기에서 만족하지 않았다. 등속도로 운동하는 관성계에만 적용되는 특수상대성이론을 완성시킨 아인슈타인은 곧 가속도를 가진 계에도 일반적으로 적용되는 일반상대성이론을 만들기 위한 새로운 여행을 시작했다.

 

 

 

관련글 :  원자와 원자핵

 

 

 

 출처: http://navercast.naver.com/science/physics/256